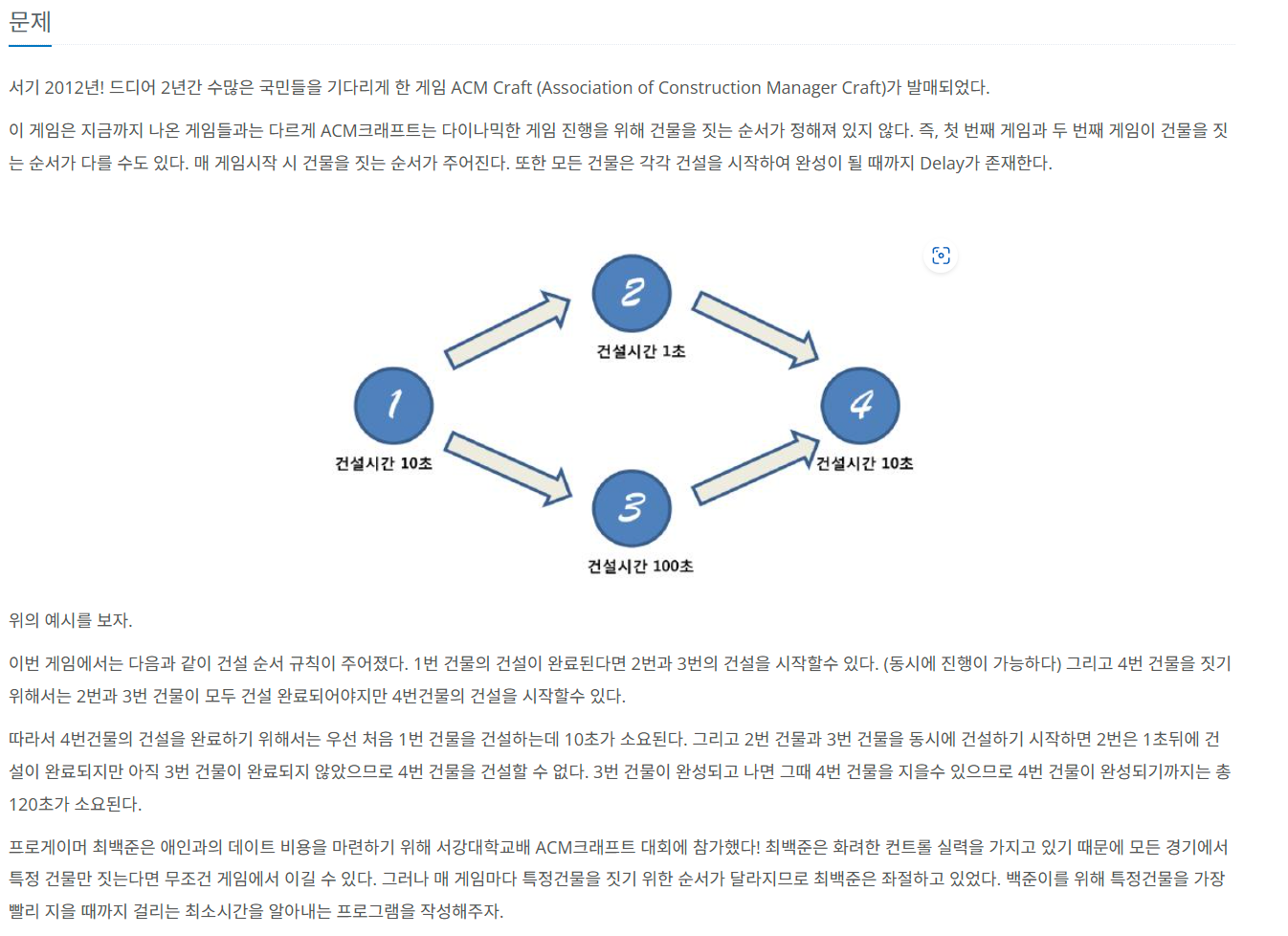
문제 해결에 사용된 개념
- 위상정렬 :
– 방향 그래프에서 각 점들을 순서대로 나열하는 방법
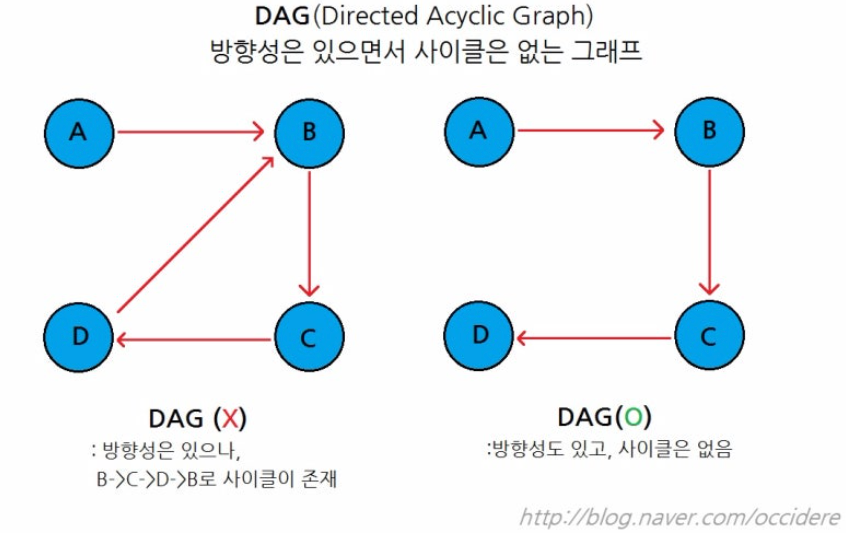
– 조건 : DAG(Directed Acyclic Graph) 그래프 방향성이 있고 사이클이 없는 그래프
– DFS를 이용한 방법과 진입차수(Indegree)를 이용한 2가지 방법이 있으나 ACM Craft에서는 건설 순서를 결정하기 위해 Indegree를 이용한 위상 정렬을 사용
- 다이나믹 프로그래밍 :
– 작은 문제들을 해결한 결과로 큰 문제를 해결하는 방법
– 중복된 계산을 줄이는 목적으로 사용됨
– ACM Craft에서는 각 도시의 건설 비용을 누적 하는데 사용됨 - 큐(Queue)
– FIFO(First In First Out) 자료 구조로 위상정렬을 구현하는데 사용
– 도시의 indegree가 0인 도시부터 처리하기 위해 큐 사용
사용된 매서드 및 시퀀스
- 위상정렬 시퀀스
– 인접 리스트 형식으로된 그래프에서 각 노드별 진입차수(indegree) 기록
– 큐 2개 생성 (탐색큐, 결과큐)
– 탐색큐에서 노드를 하나씩 poll하여 결과큐에 삽입 => 진입차수(indegree)가 0 이되면 정렬이 완료 된 것
– 탐색큐에서 poll한 노드와 연결된 노드들의 진입차수(indegree)를 -1해줌
– 진입차수 수정 후 0이 된다면 다시 탐색을 위해 탐색큐에 push
– 위 과정을 반 - void Input()
– 건물 개수와 규칙 개수를 ReadLine()
– 각 배열을 설정함 - int Output()
– Queue<int>를 사용해서 위상 정렬 수행 (FIFO)
– indegree가 0인 도시부터 시작하여, 연결된 도시들은 indegree를 감소 시키고 0이 되면 큐에 추가
– 각 도시의 최대 건설 비용 갱신
class ACM
{
//https://velog.io/@cpsn6237/3-BOJ-1005-ACM-Craft-C
private int n, k; // 총 도시, 총 규칙 개수
private int targetCity; // 도착 도시
private int[] cityCost; // 각 도시 건설 시간
private int[] dpCost; // 각 도시의 효율적인 건설 시간
private int[] indegree; // 도시의 필요한 규칙 개수
private List<int>[] nextCities; // 도시의 다음 간선(목록)
private List<int>[] prevCities; // 도시의 이전 간선(목록)
public void Input()
{
// 2. 건물개수 N , 규칙개수 K
int[] input = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
int N = input[0];
int K = input[1];
// 3. 배열 사이즈 정의
cityCost = new int[N + 1];
dpCost = new int[N + 1];
indegree = new int[N + 1];
nextCities = new List<int>[N + 1];
prevCities = new List<int>[N + 1];
// 4. 각 도시의 다음/이전 간선 리스트 초기화
for (int i = 1; i <= n; i++)
{
nextCities[i] = new List<int>();
prevCities[i] = new List<int>();
}
// 5. 각 도시의 건설 시간 입력받아 저장
var costInput = Array.ConvertAll(Console.ReadLine()!.Split(), int.Parse);
for (int i = 1; i <= n; i++)
{
cityCost[i] = costInput[i - 1];
}
// 6. 각 간선 정보 입력받아 nextCities, prevCities, indegree 배열에 반영
for (int i = 0; i < k; i++)
{
var edgeInput = Array.ConvertAll(Console.ReadLine()!.Split(), int.Parse);
nextCities[edgeInput[0]].Add(edgeInput[1]);
prevCities[edgeInput[1]].Add(edgeInput[0]);
indegree[edgeInput[1]]++;
}
// 7. 목표 도착 도시 입력받기
targetCity = int.Parse(Console.ReadLine()!);
}
public int Output()
{
var q = new Queue<int>();
// indegree가 0인 도시를 큐에 추가
for (int i = 1; i <= n; i++)
{
if (indegree[i] == 0)
q.Enqueue(i);
}
// 큐가 빌 때까지 반복
while (q.Count > 0)
{
var curCity = q.Dequeue();
// 이전 도시 중 가장 건설이 오래걸렸던 누적 비용 계산
var maxDP = 0;
foreach (int node in prevCities[curCity])
{
maxDP = Math.Max(maxDP, dpCost[node]);
}
dpCost[curCity] = maxDP + cityCost[curCity];
// 다음 도시의 indegree를 감소시키고, indegree가 0이 되면 큐에 추가
foreach (var next in nextCities[curCity])
{
indegree[next]--;
if (indegree[next] == 0)
{
q.Enqueue(next);
}
}
}
// 목표 도착 도시의 누적 건설 비용 반환
return dpCost[targetCity];
}
}
class Program
{
static void Main(string[] args)
{
// 1. 테스트 케이스
int testcase = int.Parse(Console.ReadLine());
while (testcase > 0)
{
var acm = new ACM();
acm.Input();
var result = acm.Output();
Console.WriteLine(result);
}
}
}