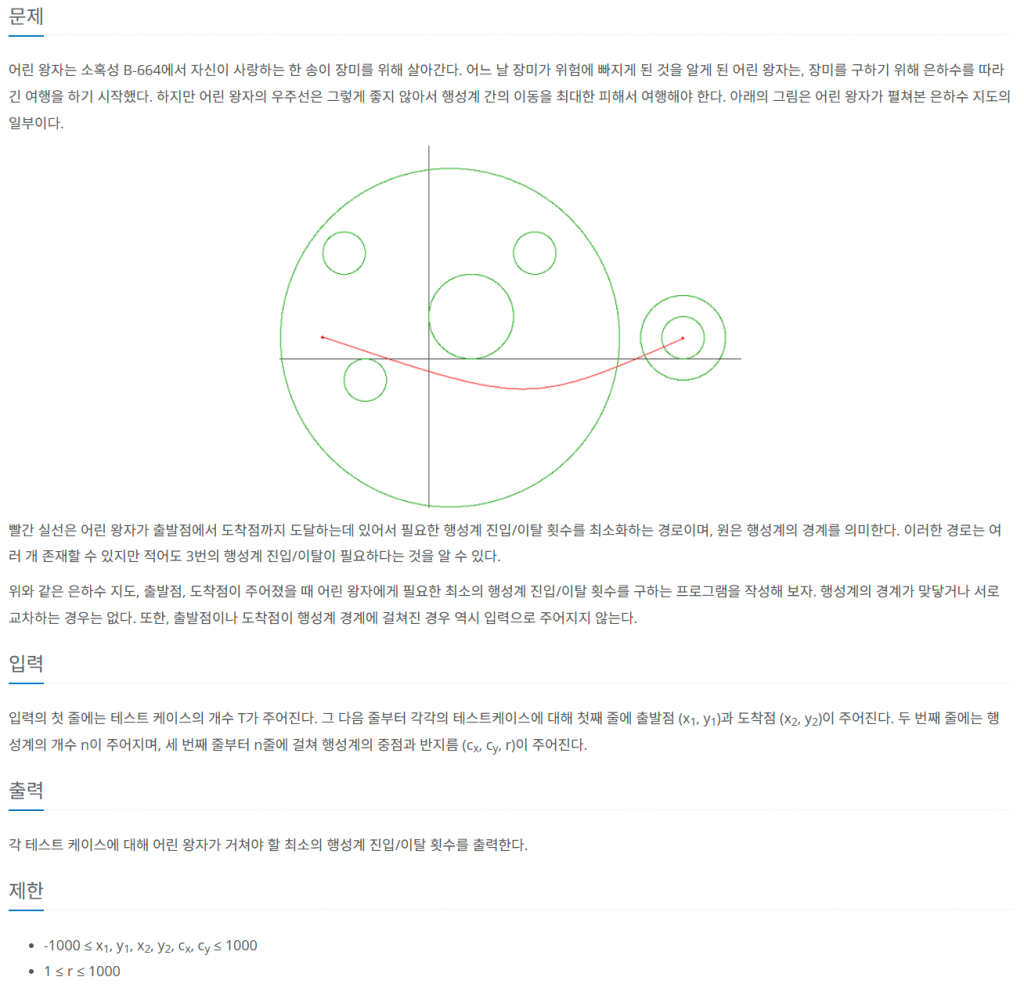
출발점부터 도착점까지 곡선이 가능하므로
초기 시작 포인트에 대해서만 고려하면 풀 수 있는 문제
백준 1002번과 같이 두개의 좌표를 알고 반지름을 알고있으면
두점사이 거리와 두원의 관계를 대입해서 풀면 된다.
우선 좌표를 ReadLine().Split()으로 입력 받는다
진입 이탈 횟수 변수도 지정해주고
입력받은 값을 출발, 도착점의 좌표로 분리해주고
행성계 갯수(n)만큼 들어오는 족족 for문으로 비교하도록 한다.
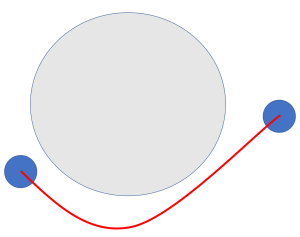
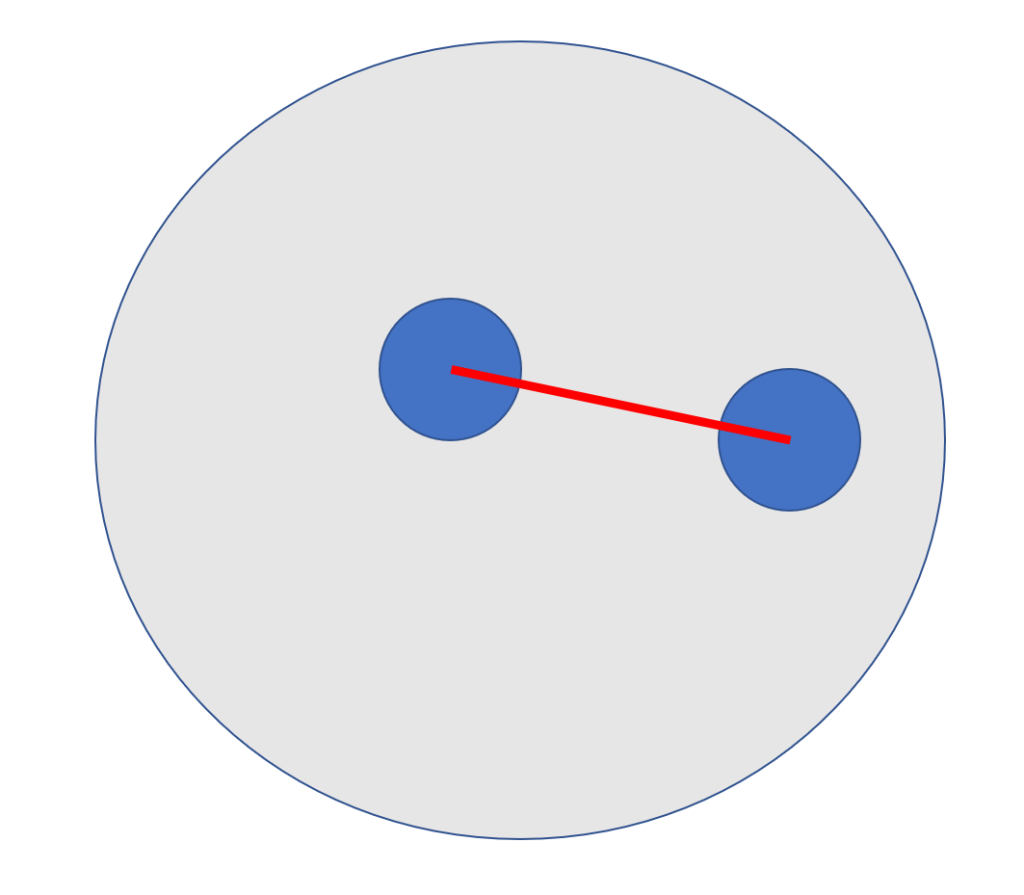
아래와 같은 두 형태는 진입/이탈 횟수에 영향을 주지 않으므로
check_1 , check_2 모두 true이거나 false 일때는 count 하지 않는다
(= check_1과 check_2가 다를때 count 한다)
class LittlePrince {
static void Main()
{
int testCase = int.Parse(Console.ReadLine());
while (testCase > 0)
{
// 출발,도착 좌표 인풋
int[] coord = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
// 진입,이탈 횟수
int count = 0;
// 출발점 좌표
int x1 = coord[0];
int y1 = coord[1];
// 도착점 좌표
int x2 = coord[2];
int y2 = coord[3];
// 행성계 개수
int n = int.Parse(Console.ReadLine());
for (int i = 0; i < n; i++)
{
// 행성계 좌표,반지름 인풋
int[] coord_c = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
// 행성계 좌표,반지름
int cx = coord_c[0];
int cy = coord_c[1];
int cr = coord_c[2];
double distance_1 = Math.Pow((x1 - cx), 2) + Math.Pow((y1 - cy), 2);
double distance_2 = Math.Pow((x2 - cx), 2) + Math.Pow((y2 - cy), 2);
//if (distance_1 <= Math.Pow(cr, 2)) count++;
//if (distance_2 <= Math.Pow(cr, 2)) count++;
// 행성계를 1개씩 비교하므로, 큰원에 2개가 다 들어있는 경우, 아예 닿지않는 경우 2가지는 count 하지 않아도 됨
bool check_1 = distance_1 < Math.Pow(cr, 2) ? true : false;
bool check_2 = distance_2 < Math.Pow(cr, 2) ? true : false;
count = check_1 != check_2 ? count+1 : count;
}
Console.WriteLine(count);
testCase--;
}
}
}
큰 항성계 안에 출발점과 도착점이 들어있는 상황을 예외 처리 하지않고 count를 직접 세다가 몇번이나 틀렸다
그래서 bool값으로 체크하고 확실히 다를때만 count 하도록 처리..
쉬운 문제 같은데도 기초가 부족하니 푸는데도 한참 걸리고 한번에 풀지도 못한다
하다보면 늘겠지..
1005번은 너무 어렵던데 또 이해하면서 푸는데 얼마나 걸릴지…